Project Description
The overall goal of this project is to provide a framework for developing model transformations, in order to resolve structural heterogeneities between metamodels. This goal can be divided into three subgoals consisting first, of a high-level mapping language (for defining a so-called mapping view) and second, of a low-level executable transformation language (for defining a so-called transformation view) and third, of a compiler that builds the bridge between these two views.
Mapping View: For realizing the mapping view, a formalism should be employed which satisfies the following requirements:
- For abstracting from implementation details, declarative model transformations are necessary.
- For building extensible model transformation libraries, reusable mapping operators are essential.
- For solving complex transformation scenarios, appropriate composition mechanisms are required.
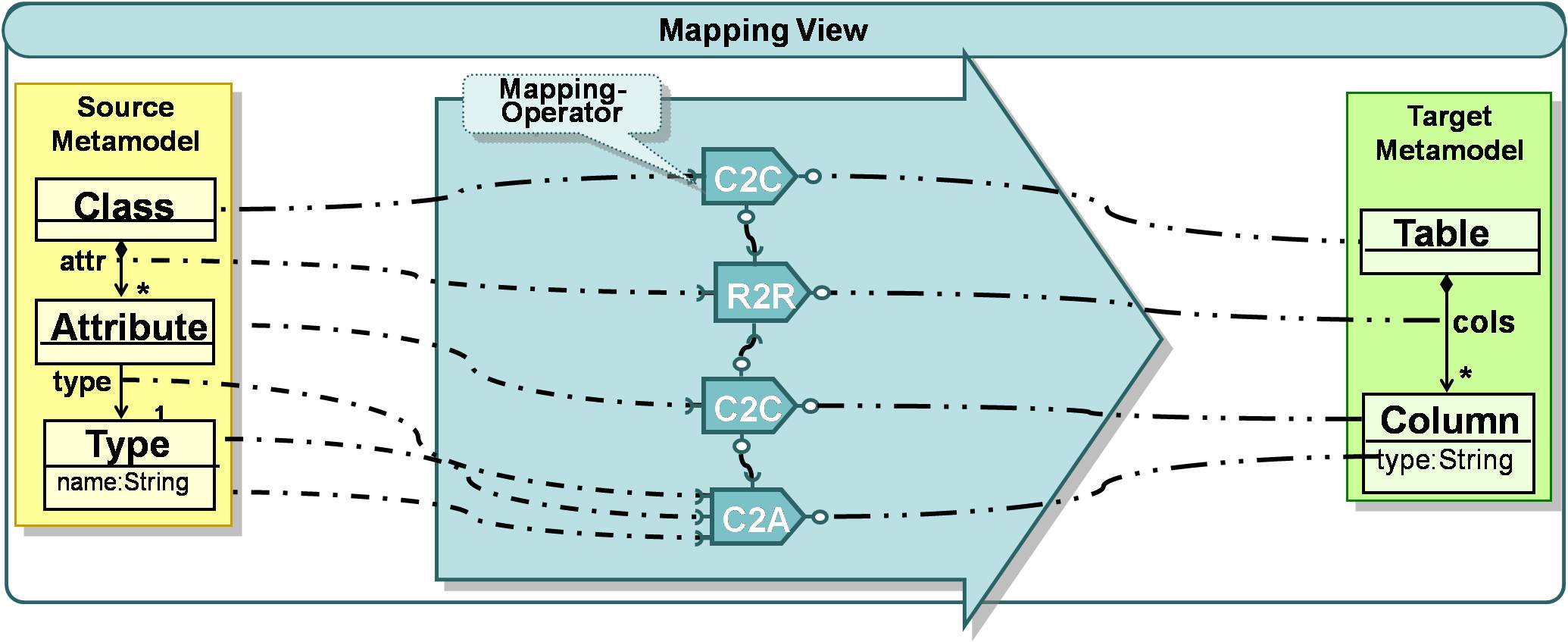
At the mapping view level, the user defines the mapping between the elements of the two metamodels (i.e. source metamodel and target metamodel). Thereby, this mapping expresses also a relationship between model elements, i.e., the instances of the metamodels (source model and target model). In the proposed approach, this mapping is defined between metamodel elements on basis of mapping operators (e.g. Class2Class – C2C-operator), standing for a processing entity encapsulating a certain kind of transformation logic. A set of applied mapping operators defines the mapping from a left hand side (LHS) metamodel to a right hand side (RHS) metamodel, further on subsumed as mapping model.
Transformation View: In order to make declarative mapping definitions executable, a formalism is necessary expressing the operational semantics of the mapping operators. We envision a formalism which fosters the analysis (i.e. understandability and debuggability) of model transformations by means of the following characteristics:
- Definition of the operational semantics of the mapping operators based on an implicit control flow.
- Provision of a homogenous representation of all the artefacts involved, i.e. metamodels, models and transformation logic itself.
- Support of a model-based representation of the transformation execution, i.e. providing an explicit and human understandable runtime model.
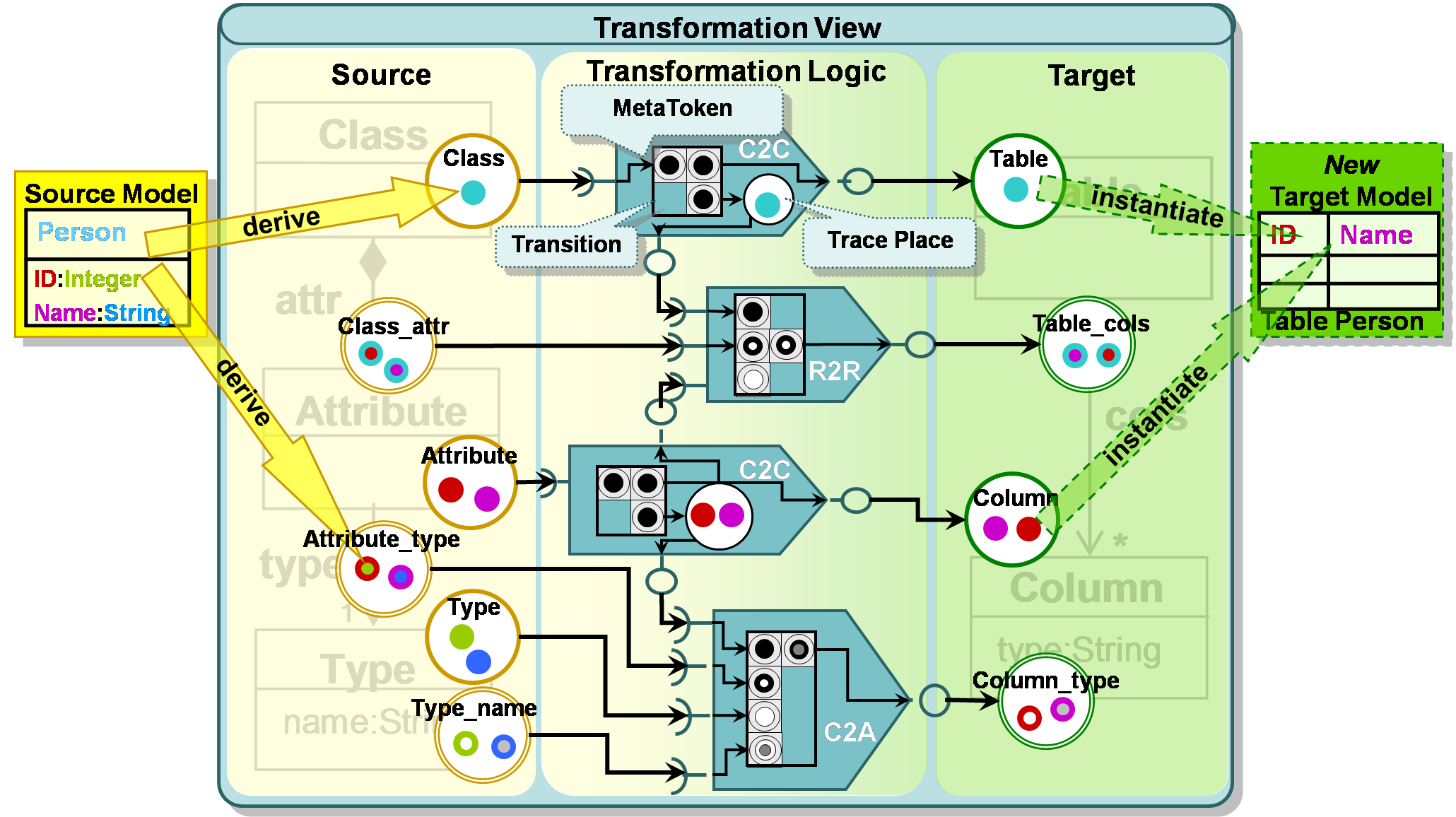
For realizing the transformation view, we are planning to use a modified form of Coloured Petri Nets, in the following denoted as Transformation Nets because of the following reasons:
- Transformation Nets enable the execution of the transformation without introducing an impedance mismatch between the mapping view and the transformation view as each mapping operator can be realized by an independent set of transitions and places without the need for an explicit control flow between the mapping operators. This results from the fact that a set of transitions and places exhibit an internal state through the tokens that are currently contained in the places. The control flow that orchestrates the mapping operators arises from these internal states, i.e. the control flow is implicit and data-driven.
- This formalism allows for a homogenous representation of all artefacts involved in a model transformation by means of a simple formalism, thus being especially suited for gaining an understanding of the intricacies of a specific model transformation.
- Since Transformation Nets are already executable an explicit runtime model is provided. Transformation Nets consist of source places at the LHS (representing the source metamodel elements) and target places at the RHS (representing the target metamodel elements). Transitions between the source and target places describe the transformation logic located in the bridging part of the Transformation Net.
Compiler: The third subgoal is providing a compiler for generating executable transformations out of declarative mapping definitions which requires appropriate means to generate executable transformation definitions out of the static parts of a mapping definition, i.e. its metamodel and model elements as well as out of the dynamic parts, i.e. the actual transformation logic.
